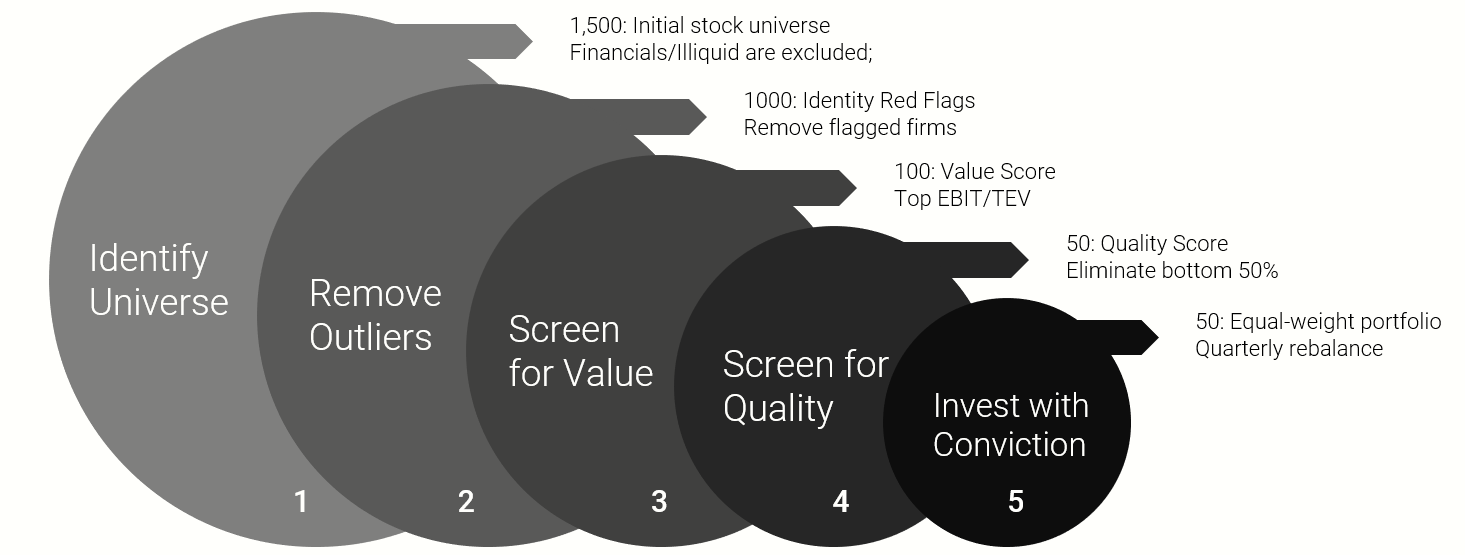
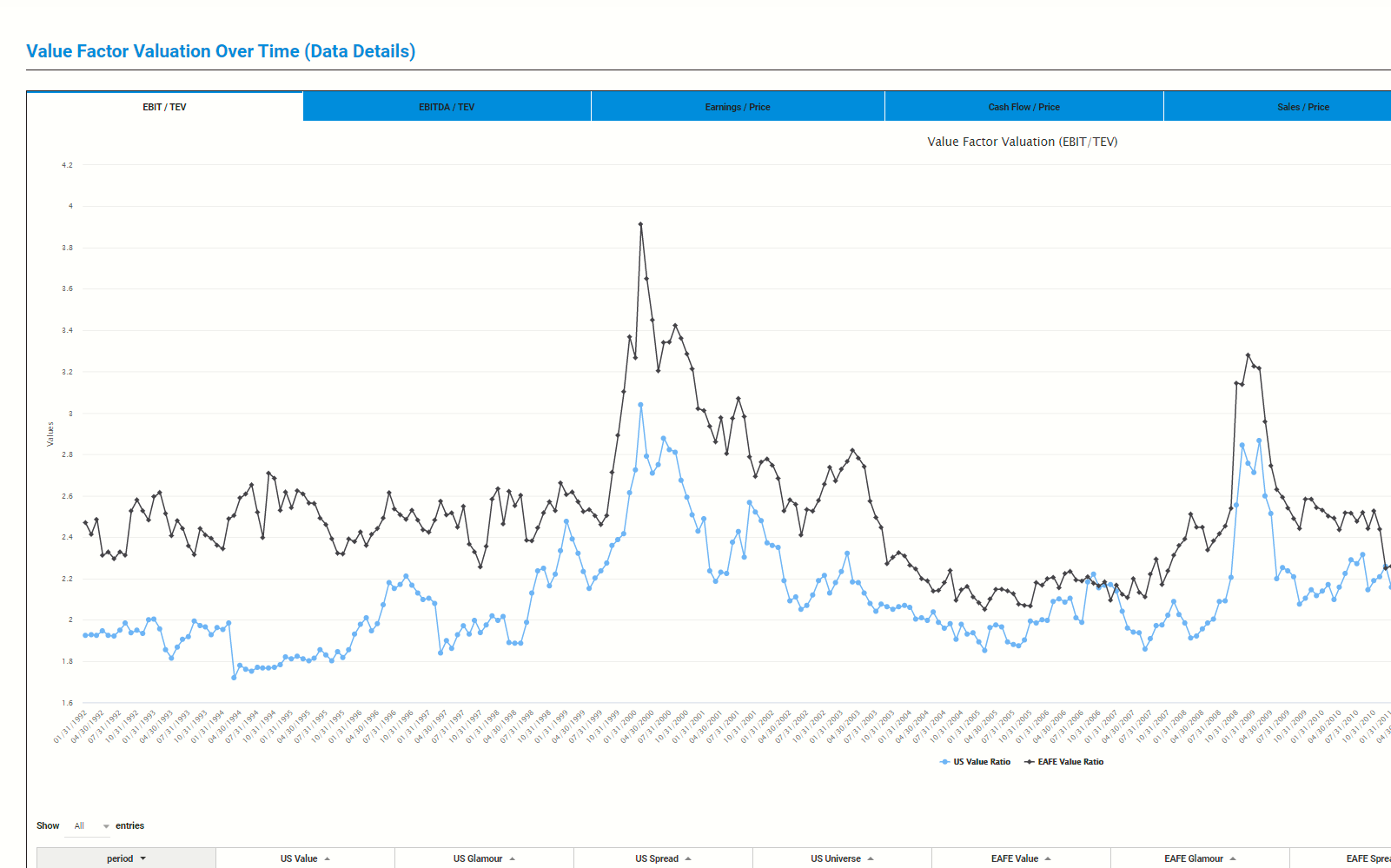
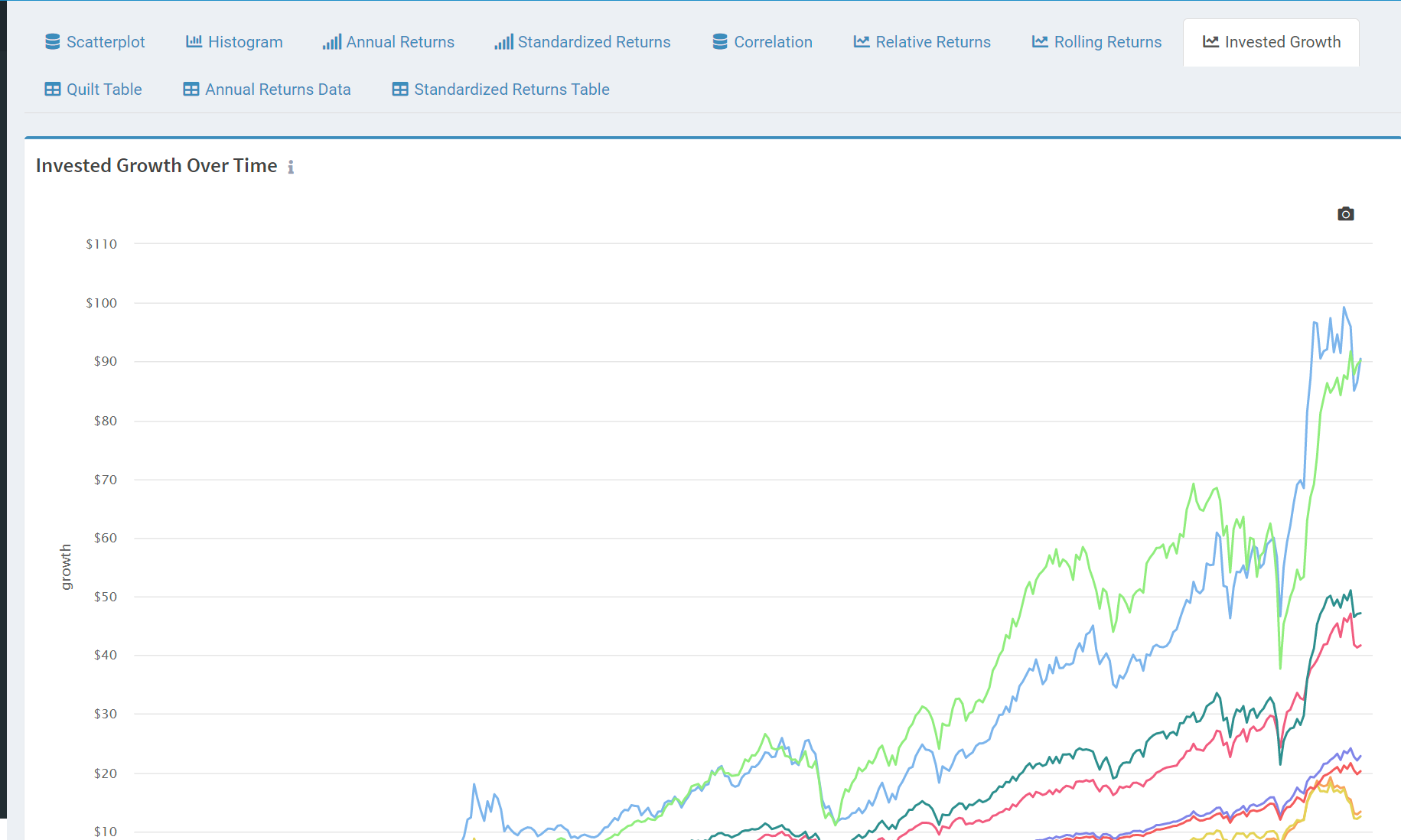
About Alpha Architect
Are You Ready to Become a Better Investor?
Get Updates Now
Important Disclosures
Performance figures contained herein are hypothetical, unaudited and prepared by Alpha Architect, LLC; hypothetical results are intended for illustrative purposes only. Past performance is not indicative of future results, which may vary. There is a risk of substantial loss associated with trading stocks, commodities, futures, options and other financial instruments. Full disclosures here.
© Copyright 2023 alpha architect | All Rights Reserved | Home | Terms of Use | Privacy Policy | Disclosures | Subscribe | Contact Us